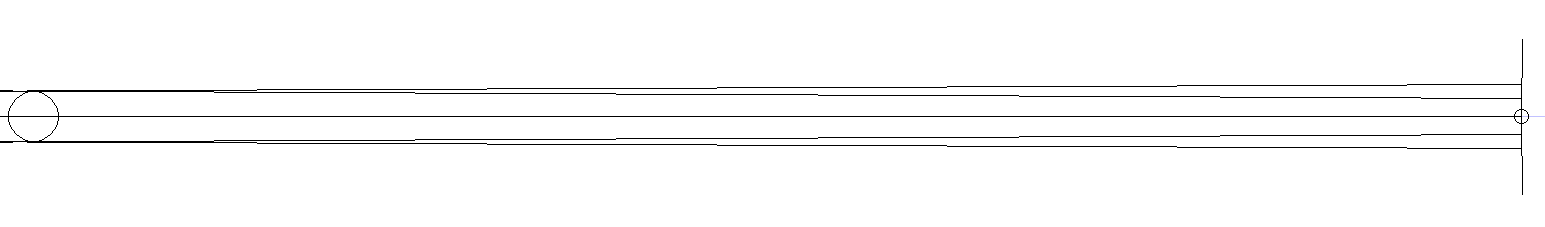There was an eclipse of the moon visible in Australia tonight.
Can you use the curvature of the earths shadow, projected onto the moon, to work out the relative size of the earth and the moon?
I suppose you can- if you know the distance between the Earth and the Moon.
AND you assume Aton (the Sun) to be at an “infinite” distance away.
But then, if you knew these, you’d probably already know what you’re seeking. ![]()
Hi @aqk ,
I suppose the biggest problem would be that the earths shadow is projected onto the curved surface of the moon, not onto a flat surface.
So the apparent curvature of the shadow would not be exactly proportional to the earths curvature.
Regards
Neville
But you’re looking at the moon as a flat surface. From the Earth, it appears as a flat surface.
I’d be more worried about the Earth being a spheroid, not a perfect sphere.
Ask your local Oblate priest.
The Moon? Perhaps it isn’t a perfect sphere either. (I never thought of this one)
Ask your local astronomer.
You are looking at a shadow on a curved surface, then the whole thing projected onto a flat plane which is the focal plane of your viewing technology.
Too complex for me.
Yes nothing is a perfect sphere.
We had an Oblate priest once, from OMI, not from Mexico.
We need to find an easier maths issue. Not much discussion on this one. Any ideas?
Regards
Neville
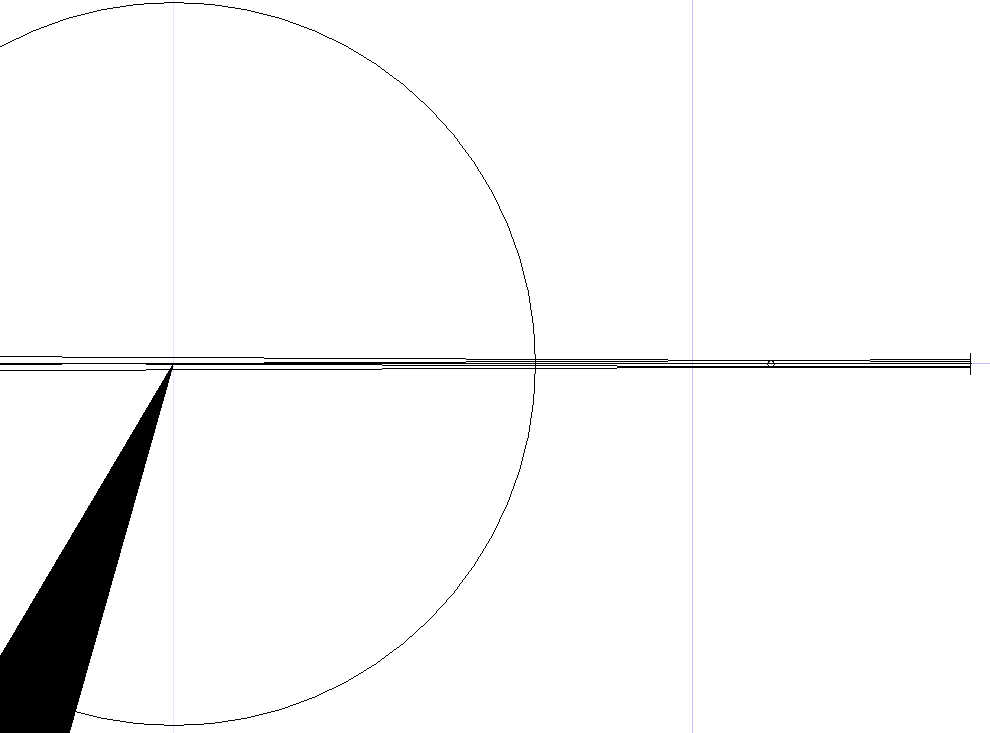
I believe that you could. This is a scale drawing of the Sun, Earth and Moon with an extra Imaginary Sun close to the earth to give an idea of scale
That’s really handy the website allowed me to spend an hour creating a reply and then told me I was only allowed to post a single image as a new user when I tried to post.
Hopefully I can add further replies.
In the above picture the squares you can see easily are actually 4 million kilometres (not sure if you will be able to see the smaller squares).
This is the imaginary sun with the Earth and Moon over to the right, and, I’ve drawn a “plane” through the moon to project the shadow of the earth.
You may not be able to see the Earth and Moon.
This is just the Earth and Moon showing the four tangents to the Sun and Earth
Includes the Plane through the moon.
@Randall ,
Hi and Welcome,
I think I get it. You are trying to allow for the change in size of the earths shadow with distance
My original thought was that the radius of the moon is proportional to the inverse of the moons curvature, and the rqdius of the earths shadow is propotional,to the inverse of the shadows curvature.
So the moons curvature divided by the shadows curvature should give the ratio of the sizes of the earth to the moon. It should be about 4.
However rhat thinking fails to allow for the expansion of the shadow as it travels from the earth to the moon. Can you work out from your diagrams, how much the shadow expands?
Regards
Neville
I wish we could do Latex in FOSS replies. It would help,to write down a bit of algebra.
I was only allowed to post three replies before so this is the last part of my original post.
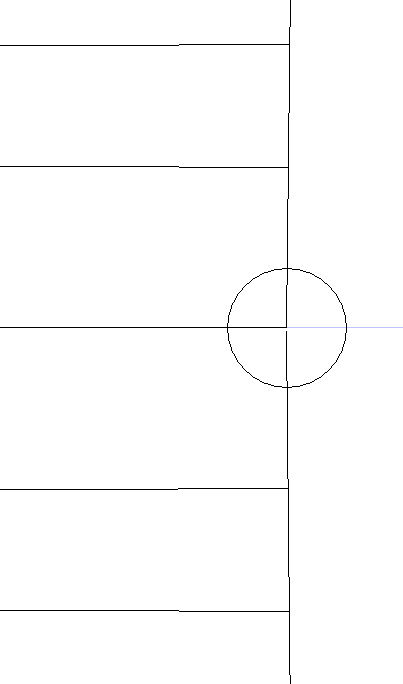
And finally just the plane through the moon showing the earth umbra and penumbra shadows
You’d need to analyse several images to measure the size of the umbra and penumbra circles relative to the moon, but, I think it could be done. (End of original post)
Don’t worry about the increase in the size of the Earth shadow from the Earth to the Moon: it’s negligible:
(Sun to Moon) / (Sun to Earth) = 148,534,400/148,150,000 = 1.0026
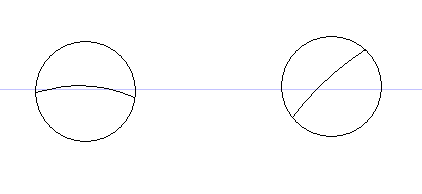
At different times the Umbra and penumbra shadows will look approximately like this
(Random orientations)
The distance sun-earth is around 400 times the distance sun-moon, so one can reasonably assume the sun is infinitely far away (depending on the precision desired). The fact that the surface of the moon is not flat does not affect significantly the calculations, as the diameter of the moon is small. So the shape of the shadow as we see it is virtually the same as if it were projected on a flat surface.
So, anyhow, at the precision that allows the shadow, with it’s blurred from the size of the source of light (the sun), the ratio of the earth and of the moon is the ratio of the radii of the shadow of the earth on the moon and of the moon itself…
They say infinity exist, I know that is a false statement. ![]()
I have just been tryong to,do exactly what you suggest, using a photo of the recent eclipse.
The shape of the earths shadow seems to increase its curvature towards the edge s of the moon, and be flatter in the centre.
I will post a photo so you can see.
Hello
I know it (infinity) exists .
Example
My mother-in-law memory_Ask Bob her hubby ![]()
Enjoy Life
artytux
I just put a period behind everyting it ended there… So infinity and beyond. ![]()
Foot squared x depth, divide by 324 tells us what? No google
Hi @silvain
I gave it a try
Here is an eclipse photo
Lets see if we can get a couple of curves to measure.
I used
Gimp and thresholded the image to obtain the following binary imageThe edge of the earths shadow seems a fairly even curve - ie it does not change curvature toward the edges.
Now we use an edge detect filter to convert it to lines
So now we have 2 curves that we can measure
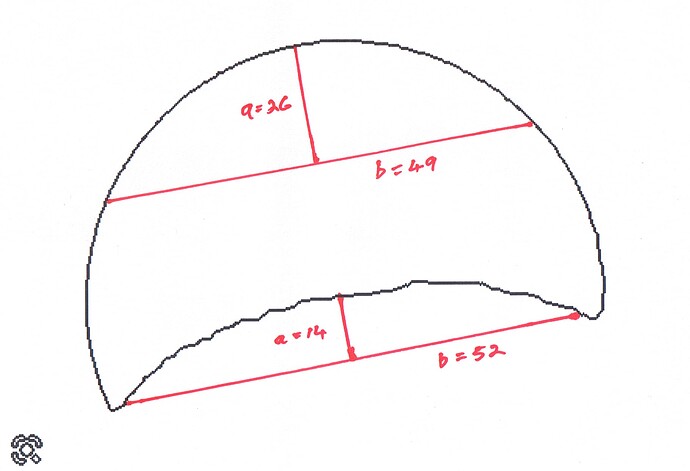
Curvature can be measured by drawing a chord to the arc, bisecting the chord and erecting a perpendicular from the chord to the arc.
If a is the height of the perpendicular line, and b is half the length of the chord, ten the radius of curvature is given by
R = (a^2 + b^2)/2a
Now the problem. Gimp will mot measure lengths of lines. It has a measure function but all it does is record coordinates of points.
So I printed the above line image and marked out my chord and perpendicular, and measured them with a ruler., as follows
Now the calculation
For the Moon
a = 26, b = 49, R = 077/52 = 59.17 (units are mm)
and the moon diameter measured with a ruler is 116mm, so radius is 58
Our method for radius of curvature is therefore correct.
For the Earth Shadow
a = 14, b = 52, R = 2900/28 = 103.57
That gives a ratio of the radii of earth to moon of 103.57/59.17 = 1.75.
Clearly wrong.
So I have to conclude that something else is influencing the apparent curvature of the earths shadow.
It may be the curvature of the moons surface is affecting the shape of the earths shadow, or it may be something else.
I remeasured just the centre part of the shadow, and got
R = (4.5^2 + 35^2)/9 = 138.36
larger, but still not nearly large enough
I dont think moons curved surface is the problem?
Regards
Neville
Hello @nevj
I tried the measure tool and maybe your way was different so posting my version if I’m wrong oops,
Measurements are taken from downloaded image completely different size but the method of measure is what I’m curious about.
So a series of tries and end result a bit on the rough side screenshot,
Was your way similar
Regards
artytux
Look at the colour of the moon in your picture: what you have calculated is the diameter of the umbra shadow. You would need another picture of the edge of the penumbra shadow. The diameter of the earth would then be the average of the umbra and penumbra shadows.
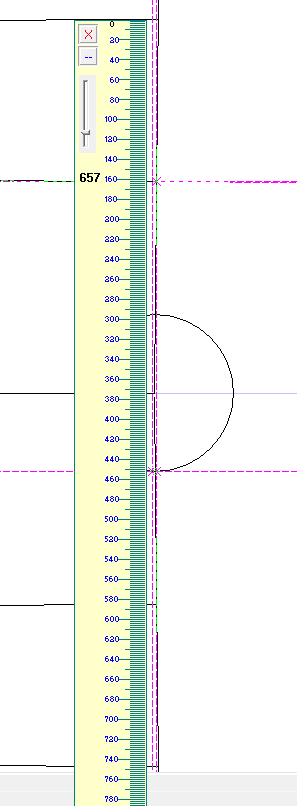
Take another look at my last picture: this time overlayed by a pixel ruler
The Penumbra shadow is 748 pixels
Umbra is 586-162 = 424 pixels
Moon is 451-295 = 156 pixels
Average of Penumbra and umbra = 586 pixels
That gives a ratio of Earth to Moon of 3.76, and, the actual ratio is 3.67 (well within the accuracy of that pixel measurement).